Algorytmy porządkowania liczb to zestaw metod służących do uporządkowania zbioru liczb w określonej kolejności, np. rosnącej lub malejącej. Są fundamentem wielu zastosowań informatycznych, takich jak zarządzanie danymi czy optymalizacja wyszukiwań. Oto krótkie omówienie najpopularniejszych algorytmów:
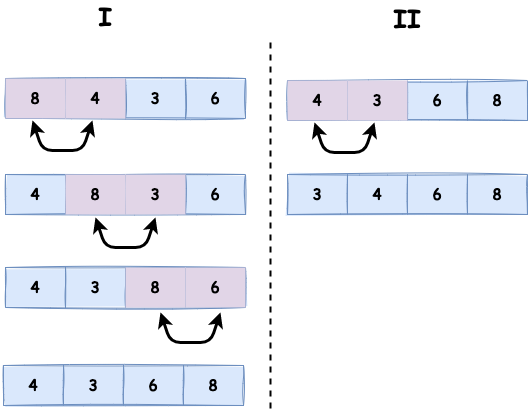
Metoda bąbelkowa
To najprostszy sposób sortowania, w którym sąsiednie elementy są porównywane i zamieniane miejscami, jeśli są w złej kolejności.
Kroki algorytmu:
- Przejdź przez tablicę.
- Porównaj dwa kolejne elementy i zamień je, jeśli są w złej kolejności.
- Powtarzaj aż do momentu, gdy cała tablica będzie posortowana.
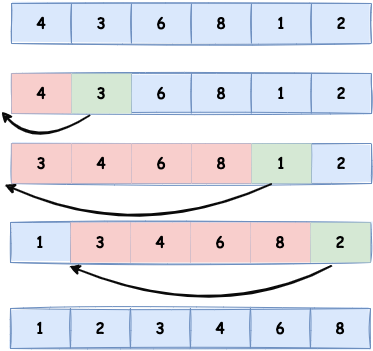
Porządkowanie przez wstawianie
Każdy element jest wstawiany na odpowiednie miejsce w już posortowanej części tablicy.
Złożoność:
- Najlepszy przypadek (tablica już posortowana): O(n)O(n)O(n).
- Najgorszy przypadek: O(n2)O(n^2)O(n2).
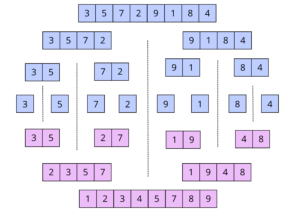
Metoda połowienia (merge sort)
Polega na dzieleniu tablicy na mniejsze części, sortowaniu ich i scalaniu.
Kroki algorytmu:
- Podziel tablicę na dwie części.
- Posortuj każdą część rekurencyjnie.
- Połącz posortowane części.
Złożoność:
- Stała: O(nlogn)O(n \log n)O(nlogn).
Wieże Hanoi
To klasyczny problem polegający na przenoszeniu nnn krążków z jednego słupka na inny przy użyciu słupka pomocniczego, przestrzegając reguł:
- Na mniejszym krążku nie może znajdować się większy.
- Można przenosić tylko jeden krążek naraz.
Rekurencyjny schemat:
- Przenieś n−1n-1n−1 krążków na słupek pomocniczy.
- Przenieś największy krążek na docelowy.
- Przenieś n−1n-1n−1 krążków ze słupka pomocniczego na docelowy.
Liczba ruchów:
2n−12^n – 12n−1, gdzie nnn to liczba krążków.
Przykładowa gra wież Hanoi :